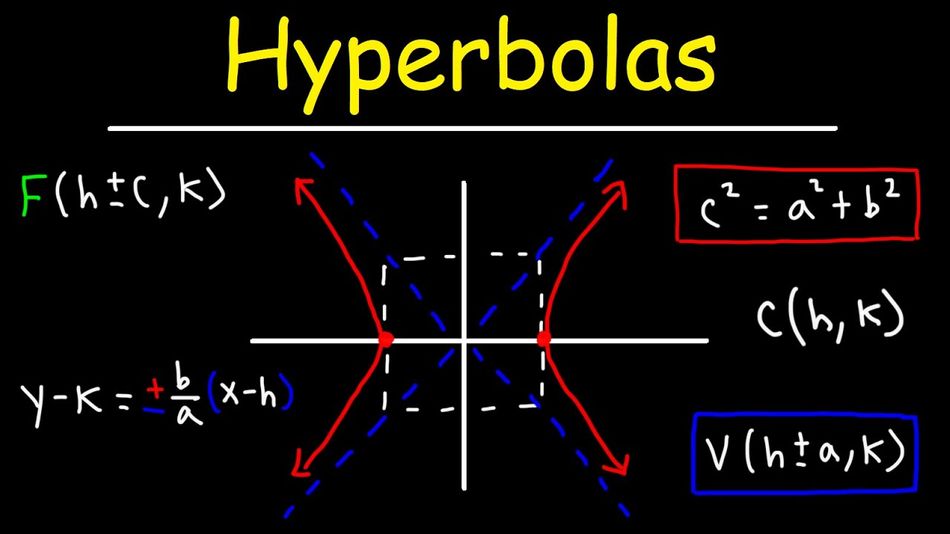
In the subject of mathematics, a hyperbola is defined as a kind of curve that is smooth and resting in a plane. It consists of 2 parts termed joints or branches, which resemble each other and are in the shape of bows that are infinite in nature. One of the 3 types of conics sections is a hyperbola.
A hyperbola is obtained when the intersection of a plane and a cone takes place. The term hyperbola is derived from the Greek word meaning “excessive”. The rest of the conic sections include the parabola and the ellipse. The alternate definition of a hyperbola is the figure acquired when a plane intersects the halves of the double cone but doesn’t traverse the cones’ apex. Every limb of a hyperbola has 2 arms that are straight farther out from the hyperbola’s centre. The arms are diagonally opposite, one arising from each arm, tend in the limit to a line that is common, termed asymptote of the 2 limbs. There exist 2 asymptotes whose convergence is at the middle of the symmetry of the hyperbola, which can be assumed as the point that is alike about which each limb reflects to structure the other limb.
They share most of the analytical properties of the ellipse namely, eccentricity, focus and directrix. A lot of mathematical items find their origin in the conic section, hyperbola, namely saddle surfaces, hyperboloids, hyperbolic functions and hyperbolic geometry. The discovery of hyperbola happened during the examination of the problem of cube doubling, but was then termed cone’s obtuse sections. It is believed that the word hyperbola was introduced by Greek geometer Apollonius of Perga in his work that consists of conic sections. The rest of the conic sections, the ellipse and parabola, are coined from Greek words meaning “applied” and “deficient”. All 3 names are taken from earlier Pythagorean phraseology that refers to a comparison of the rectangle’s sides with an area that is fixed along with a line segment given.
The standard equations of the hyperbola are
1] (x2 / a2) – (y2 / b2) = 1 consists of the transverse axis as its x-axis and the conjugate axis is the y-axis.
2] (y2 / a2) – (x2 / b2) = 1 consists of the transverse axis as its y-axis and its conjugate axis as its x-axis.
Problems on Hyperbola
Problem 1: The hyperbola equation is [(x – 5)2 / 42] – [(y – 2)2 / 62] = 1. What is the
asymptote of the hyperbola?
Answer:
The hyperbola equation is [(x – 5)2 / 42] – [(y – 2)2 / 62] = 1.
From one of the formulae of asymptotes,
![]()
y = 2 – (6 / 4) x + (6 / 4) 5 and y = 2 + (6 / 4) x – (6 / 4) 5
The asymptotes are given by y = 2 – (3 / 2) x + (3 / 2) 5, and y = 2 + (3 / 2) x – (3 / 2) 5.
Problem 2: The equation of the hyperbola is [(x – 5)2 / 62] – [(y – 2)2 / 42] = 1. Find the length of the major axis and minor axis.
Answer:
The equation of the hyperbola is [(x – 5)2 / 62] – [(y – 2)2 / 42] = 1.
Here the value a = 6 and value of b = 4.
By using the formula to find the length of the major axis and minor axis,
Length of major axis = 2a, and length of minor axis = 2b
Length of major axis = 2 × 6 = 12 units, and length of minor axis = 2 × 4 = 8 units
The length of the major axis is 12 units, and the length of the minor axis is 8 units.